认识复杂度
- 评估算法优劣的核心指标是什么？
- 时间复杂度（流程决定）
- 额外空间复杂度（流程决定）
- 常数项时间（实现细节决定）
- 什么是常数项时间？
- 数组的寻址操作，是一个常数项时间操作，每次执行时间都是固定时间，与数据量的大小无关.
- 常见的常数时间的操作
- 常见的算数运算（+、-、*、/、%等）
- 常见的位运算
[带符号位，统一右移，然后看符号位是什么就用什么补]、>>>[不带符号位]、<<、|、&、^等）
- 赋值、比较、自增、自减操作等
- 数组寻址操作
- 反例:Java:LinkedList:这个在底层属于双向链表，如果你要list.get(5)，那么并不会像数组寻址那样直接计算偏移量，而是一个一个地去遍历，到了合适的位置才取值，这个就不是常数项时间。
- 执行时间固定的操作,就是常数时间的操作.
- 执行时间不固定的操作,都不是常数时间的操作.
时间复杂度
- 定性描述该算法的运行时间
- 如何确定算法流程的总操作数量与样本数量之间的表达式关系？
- 想象该算法流程所处理的数据状况，要按照最差的情况来。
- 把整个流程彻底拆分为一个个基本动作，保证每个动作都是常数时间的操作。
- 如果数据量为N，看看基本动作的数量和N是什么关系。
- 时间复杂度怎么表达？
- 当完成了表达式的建立后，只要把最高阶项留下即可。低阶项都去掉，高阶项的系数也要去掉，记为O(忽略掉系数的高阶项)
- 时间复杂度的意义？
- 时间复杂度是衡量算法流程复杂程度的一种指标，这个指标只与数据量有关，与过程之外的优化无关.
- O(1) < O(logN) < O(N) < O(N*logN) < O(N^2) < … < O(N^k) < O(2^n) < … < O(k^n) < O(n!)
额外空间复杂度
- 什么是空间复杂度？
- 你要实现一个算法流程，在实现算法流程的过程中，你需要开辟一些空间来支持你的算法流程。作为输入参数的空间，不算额外空间，作为输出结果的空间，也不算额外空间。因为这些都是必要的，和现实目标有关的，所以都不算。但是除此之外，你的流程如果还需要开辟空间才能让你的流程继续下去，这部分空间就是额外空间，如果你的流程只需要开辟有限几个变量，额外空间复杂度就是O(1)。
- 最优解,什么是最优解？
- 时间复杂度尽可能得低，
- 先满足了时间复杂度最低这个指标之后，使用最少的空间的算法流程，叫做这个问题的最优解。
- 一般来说最优解都是忽略掉常数项这个因素的，因为这个因素只决定了实现层次的优化和考虑，而和怎么解决整个问题的思想无关。
认识对数器
- 你想要测的方法a。
- 实现复杂度不好但是容易实现的方法b。
- 实现一个随机样本产生器。
- 把方法a和方法b跑相同的随机样本，看看得到的结果是否一样。
- 如果有一个随机样本使得比对结果不一致，打印样本进行人工干预，改对方法a和方法b。
- 当样本数量很多时比对测试依然正确，可以确定方法a已经正确。
二分法O(logN)
- 在一个有序数组中，找某个数是否存在
public static boolean exist(int[] sortedArr, int num) {
if (sortedArr == null || sortedArr.length == 0) {
return false;
}
int L = 0;
int R = sortedArr.length - 1;
int mid = 0;
// L..R
while (L < R) {
// L..R 至少两个数的时候
// mid = (L+R) / 2;
// L 10亿 R 18亿
// mid = L + (R - L) / 2
// N / 2 N >> 1
// X*2+1可以表示为( X<<2 | 1 )
// mid = (L + R) / 2
mid = L + ((R - L) >> 1);
if (sortedArr[mid] == num) {
return true;
} else if (sortedArr[mid] > num) {
R = mid - 1;
} else {
L = mid + 1;
}
}
return sortedArr[L] == num;
}
- 在一个有序数组中，找>=某个数最左侧的位置
// 在arr上，找满足>=value的最左位置
public static int nearestIndex(int[] arr, int value) {
int L = 0;
int R = arr.length - 1;
int index = -1; // 记录最左的对号
while (L <= R) { // 至少一个数的时候
int mid = L + ((R - L) >> 1);
if (arr[mid] >= value) {
index = mid;
R = mid - 1;
} else {
L = mid + 1;
}
}
return index;
}
- 在一个有序数组中，找<=某个数最右侧的位置
// 在arr上，找满足<=value的最右位置
public static int nearestIndex(int[] arr, int value) {
int L = 0;
int R = arr.length - 1;
int index = -1; // 记录最右的对号
while (L <= R) {
int mid = L + ((R - L) >> 1);
if (arr[mid] <= value) {
index = mid;
L = mid + 1;
} else {
R = mid - 1;
}
}
return index;
}
- 局部最小值问题(返回一个局部最小值就好)
- 只要知道左右有一侧可以有结果,就可以舍去另一侧,就可以二分
// 课上的代码
public static int getLessIndex(int[] arr) {
if (arr == null || arr.length == 0) {
return -1;
}
if (arr.length == 1 || arr[0] < arr[1]) {
return 0;
}
if (arr[arr.length - 1] < arr[arr.length - 2]) {
return arr.length - 1;
}
// 到了这里，我们就明白趋势了。先下后上，所以一定会存在最小值。
int left = 1;
int right = arr.length - 2;
int mid = 0;
while (left < right) {
mid = (left + right) / 2;
if (arr[mid] > arr[mid - 1]) {
right = mid - 1;
} else if (arr[mid] > arr[mid + 1]) {
left = mid + 1;
} else {
return mid;
}
}
return left;
}
- 补充知识
- N*2 可以写作 N<<1
- N*2+1 可以写作 (N<<1)|1
认识异或运算
- 异或运算（^）：相同则0，不同则1；同或运算（⊙）：相同则1，不同则0。
- 能长时间记住的概率接近0%，所以，异或运算就记成无进位相加
- （无进位是什么意思？就是二进制去相加，即便两者都是1，相加结果是2，不要进位，也就是得到0且不要进位）。
- 异或运算的性质
- 0^N == N、N^N == 0。
- 异或运算满足交换律和结合律。
- 上面的两个性质用无进位相加来理解就非常得容易。
- 例子:
- 如何不需要额外的变量即可实现两个数字的交换(但是特别注意，只有两个变量用的不是同一个内存的时候才可以这样干！)
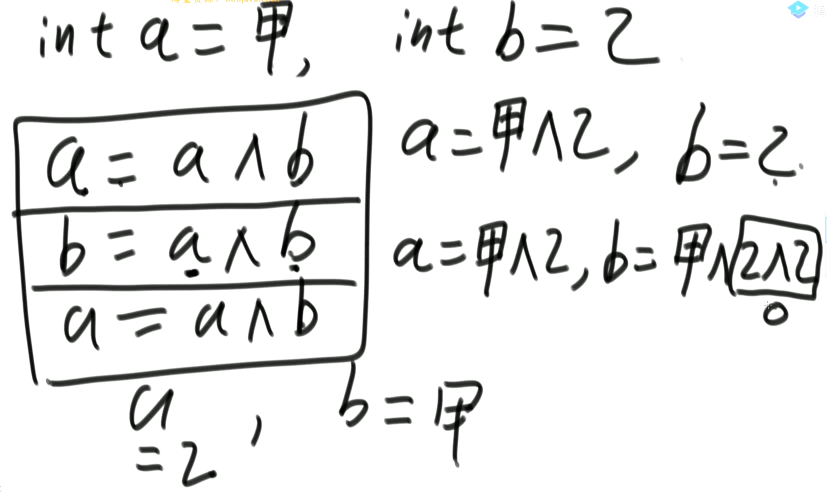
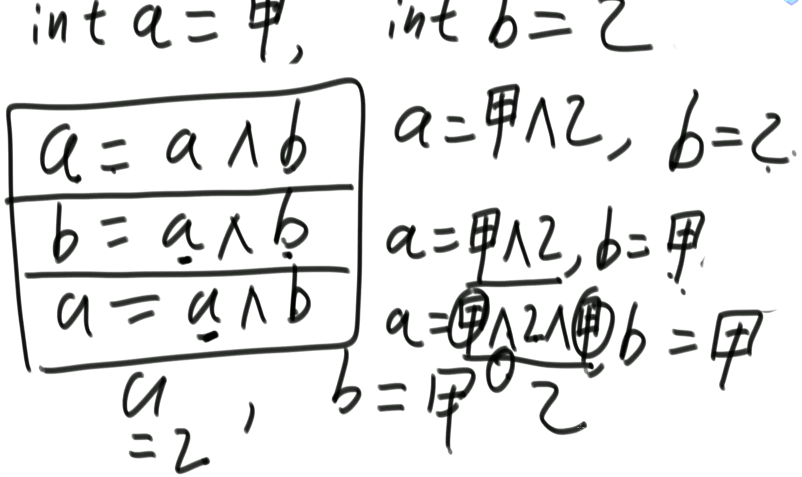
public class Test01 {
public static void main(String[] args) {
// 如何不需要额外的变量即可实现两个数字的交换，但是特别注意，只有两个变量用的不是同一个内存的时候才可以这样干！
int a = 10;
int b = 4;
a = a ^ b;
b = a ^ b;
a = a ^ b;
// b = a ^ b ^ b = a ^ 0 = a; 运用交换律和结合律
// a = a ^ b = a ^ b ^ a ^ b ^ b = a ^ a ^ b ^ b ^ b = b; 运用交换律和结合律
System.out.println("a=" + a + ",b=" + b);
}
}
- 一个数组中有一种数出现了奇数次，其他数都出现了偶数次，怎么找到并打印这个数字？
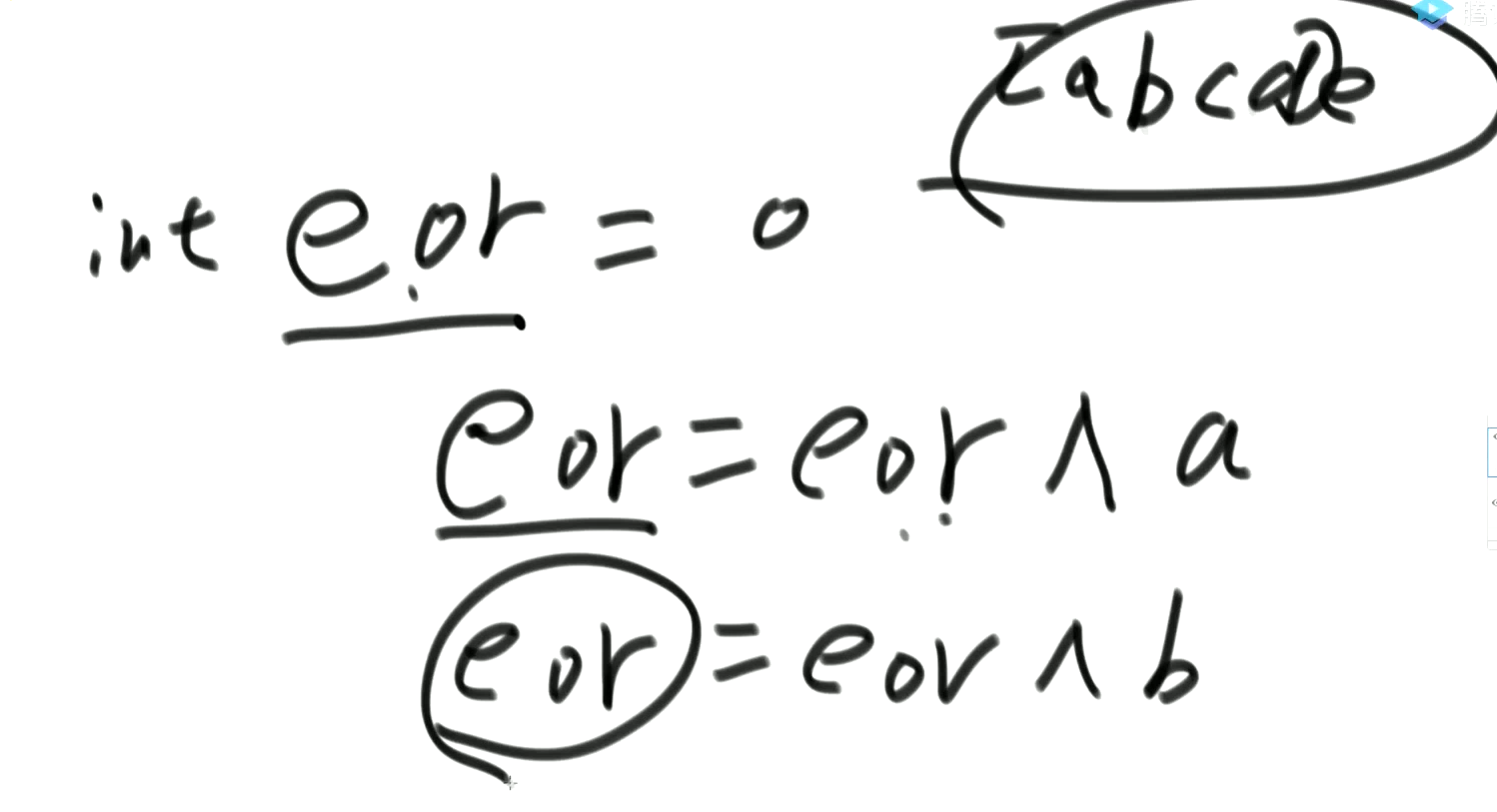
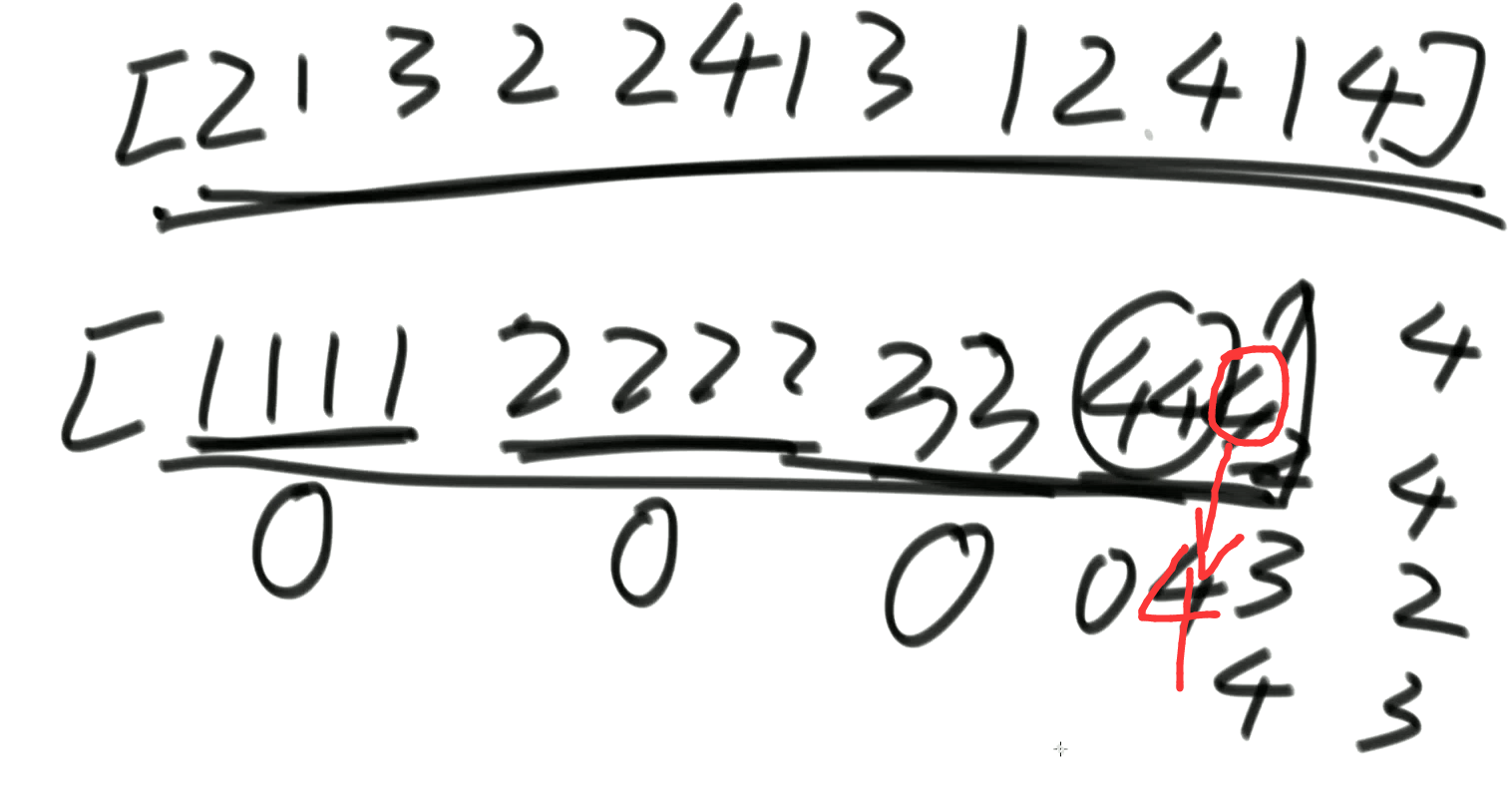
public class Test {
// 一个数组中有一种数出现了奇数次，其他数都出现了偶数次，怎么找到并打印这个数字？
public static void printOddTimesNum1(int[] arr){
int eor = arr[0];
for(int i = 1; i < arr.length;i++){
eor ^= arr[i];
}
System.out.println(eor);
}
public static void main(String[] args) {
int[] arr = new int[]{1,1,2,2,3,3,4};
printOddTimesNum1(arr);
}
}
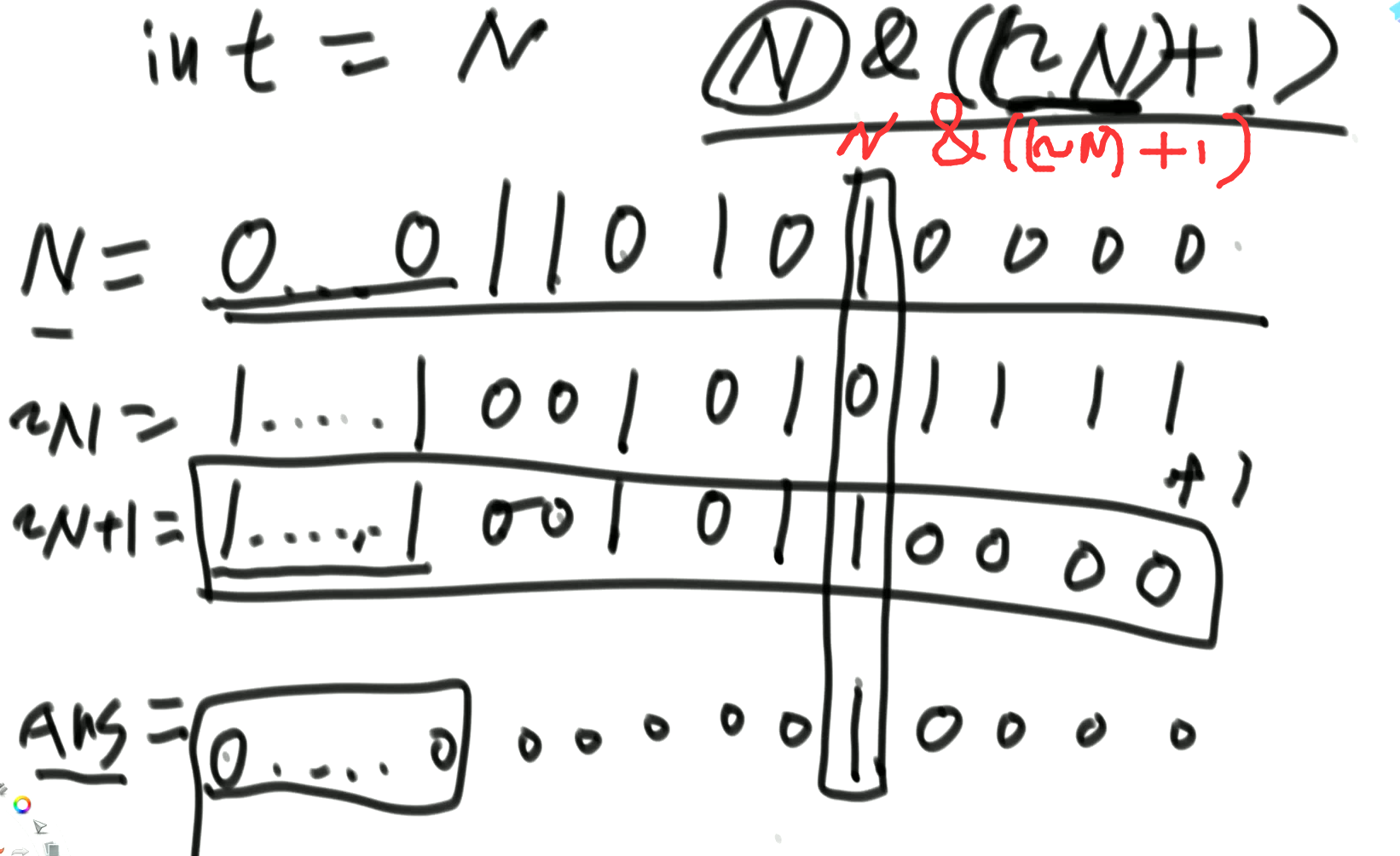
- 怎么把一个整数，提取出最右侧的1来
public class Test {
// 怎么把一个整数，提取出最右侧的1来
public static int func(int number){
// 00000011 01010000
// 11111100 10101111 （取反）
// 11111100 10110000 （加1）
// 00000000 00010000 （与）
return number & ((~number) + 1);
}
public static void main(String[] args) {
int num = 234;
System.out.println(func(num));
}
}
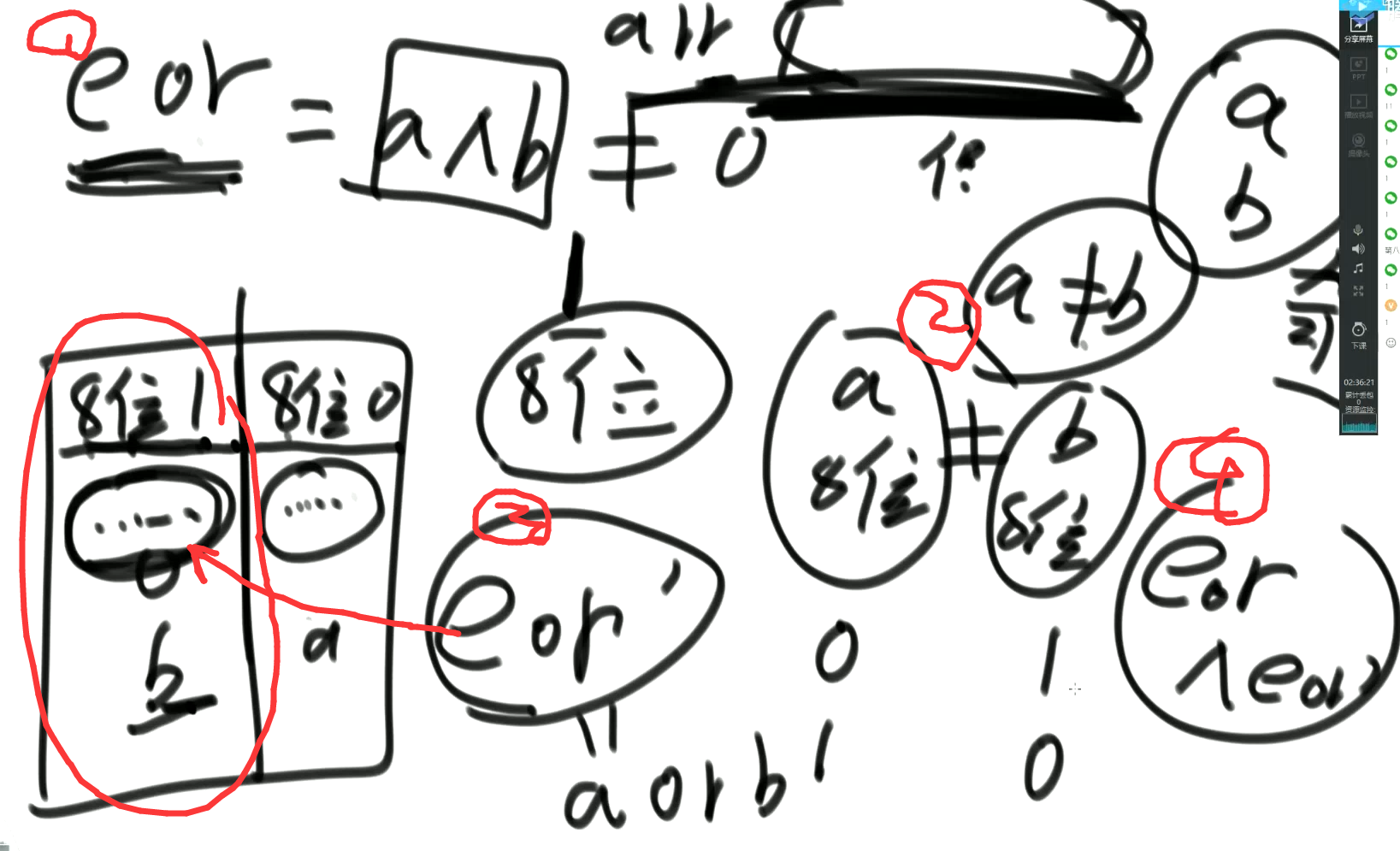
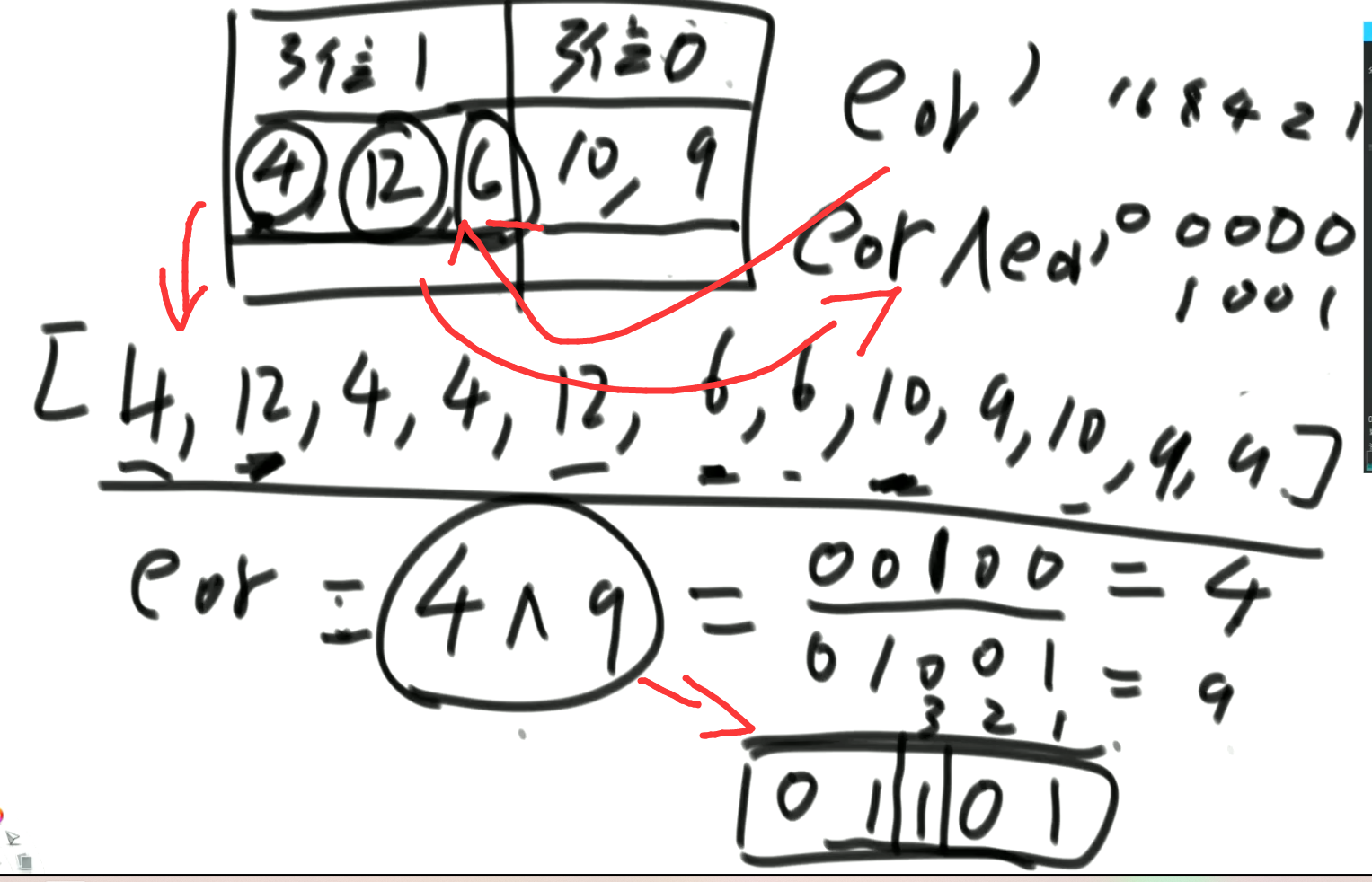
- arr中，有两种数，出现奇数次
public class Test {
// arr中，有两种数，出现奇数次
public static void printOddTimesNum2(int[] arr) {
int eor = 0;
for (int i = 0; i < arr.length; i++) {
eor ^= arr[i];
}
// eor = a ^ b
// eor != 0
// eor必然有一个位置上是1
// 0110010000
// 0000010000
int rightOne = eor & (~eor + 1); // 提取出最右的1
int onlyOne = 0; // eor'
for (int i = 0 ; i < arr.length;i++) {
// arr[1] = 111100011110000
// rightOne= 000000000010000
if ((arr[i] & rightOne) != 0) {
onlyOne ^= arr[i];
}
}
System.out.println(onlyOne + " " + (eor ^ onlyOne));
}
public static void main(String[] args) {
}
}
- 看一个数字的二进制样式中有几个1
public class Test {
// 看一个数字的二进制样式中有几个1
public static int func(int num){
int count = 0;
while(num != 0){
int rightOne = num & ((~num) + 1);
count++;
num ^= rightOne;
}
return count;
}
public static void main(String[] args) {
int num = 234;
System.out.println(func(num));
}
}
转载请注明来源，欢迎对文章中的引用来源进行考证，欢迎指出任何有错误或不够清晰的表达，可以邮件至 963614756@qq.com。