暴力递归到动态优化

我要就业
Created At :
Count:3.7k Views 👀 :
  1. 常见的4种尝试模型
  2. 暴力递归到动态规划的总纲
  3. 暴力递归实现斐波那契数列
  4. 机器人找位置
  5. 从左往右尝试模型:背包问题:
  6. 从左往右尝试模型:数字字符转化问题
  7. 范围上的尝试模型:玩家抽取纸牌问题
  8. 暴力递归到动态规划
  9. 凑货币问题（重要）:该题是对动态规划完整优化路径的演示
  10. 贴纸问题
  11. 面试中设计暴力递归过程的原则
  12. 笔试面试过程中怎么设计暴力递归？
  13. 常见的4种尝试模型
  14. 如何分析有没有重复解
  15. 暴力递归到动态规划的套路
  16. 动态规划的进一步优化
  17. 多样本位置全对应的尝试模型:两个字符串的最长公共子序列
  18. 寻找业务限制的尝试模型:咖啡问题

常见的4种尝试模型

  1. 从左往右的尝试模型
  2. 范围上的尝试模型
  3. 多样本位置全对应的尝试模型
  4. 寻找业务限制的尝试模型

暴力递归到动态规划的总纲

  1. 尝试 ==> 分辨出来所有的参数，找到所有的可变参数以及固定的值（边界）
  2. 可变参数的组合是什么，表大小根据可变参数的变化范围来确定
  3. 已知固定位置的依赖，有具体参数的例子（范围的两端）
  4. 知道在表中的最终想要的位置，baseCase固定的行列（确定好baseCase）
  5. 分析任意位置的依赖

暴力递归实现斐波那契数列

机器人找位置

  1. 动态规划(记忆化搜索)：你的暴力递归过程有重复计算,我给你加缓存,下次遇到同样过程直接给你解
  2. 经典的动态规划:把整个DP表从简单状态到复杂状态都列出来
  3. 从暴力递归改动态规划,不用看原题意,看暴力递归过程,足矣
  4. 题目解释
    1. 假设有排成一行的N个位置记为1~N，N一定大于或等于2
    2. 开始时机器人在其中的M位置上(M一定是1~N中的一个)
    3. 如果机器人来到1位置，那么下一步只能往右来到2位置；
    4. 如果机器人来到N位置，那么下一步只能往左来到N-1位置；
    5. 如果机器人来到中间位置，那么下一步可以往左走或者往右走；
    6. 规定机器人必须走K步，最终能来到P位置(P也是1~N中的一个)的方法有多少种
    7. 给定四个参数 N、M、K、P，返回方法数
  5. 传统递归:
    public static int robotWalkRegularRecursion(int N, int start, int aim, int K) {
    if (N < 2 || start < 1 || start > N || aim < 1 || aim > N || K < 1) {
        return -1;
    }
    return process1(start, K, aim, N);
}

// 机器人当前来到的位置是cur，
// 机器人还有rest步需要去走，
// 最终的目标是aim，
// 有哪些位置？1~N
// 返回：机器人从cur出发，走过rest步之后，最终停在aim的方法数，是多少？
public static int process1(int cur, int rest, int aim, int N) {
    if (rest == 0) { // 如果已经不需要走了，走完了！
        return cur == aim ? 1 : 0;
    }
    if (cur == 1) { // 1 -> 2
        return process1(2, rest - 1, aim, N);
    }
    if (cur == N) { // N-1 <- N
        return process1(N - 1, rest - 1, aim, N);
    }
    return process1(cur - 1, rest - 1, aim, N)
            + process1(cur + 1, rest - 1, aim, N);
}
  6. 动态规划(记忆化搜索)
    // 动态规划(记忆化搜索)：你的暴力递归过程有重复计算,我给你加缓存,下次遇到同样过程直接给你解
// 如果把整个DP表从简单状态到复杂状态都列出来,就是经典的动态规划
// dp就是缓存表
// dp[cur][rest] == -1 -> process1(cur, rest)之前没算过！
// dp[cur][rest] != -1 -> process1(cur, rest)之前算过！返回值，dp[cur][rest]
// N+1 * K+1
public static int robotWalkMemoryDP(int N, int start, int aim, int K) {
    if (N < 2 || start < 1 || start > N || aim < 1 || aim > N || K < 1) {
        return -1;
    }
    int[][] dp = new int[N + 1][K + 1];
    for (int i = 0; i <= N; i++) {
        for (int j = 0; j <= K; j++) {
            dp[i][j] = -1;
        }
    }
    return walkCache(start, K, aim, N, dp);
}

// cur 范: 1 ~ N
// rest 范：0 ~ K
public static int walkCache(int cur, int rest, int aim, int N, int[][] dp) {
    // 如果之前算过了,直接出来结果
    if (dp[cur][rest] != -1) {
        return dp[cur][rest];
    }
    // 之前没算过！
    int ans = 0;
    if (rest == 0) {
        ans = cur == aim ? 1 : 0;
    } else if (cur == 1) {
        ans = walkCache(2, rest - 1, aim, N, dp);
    } else if (cur == N) {
        ans = walkCache(N - 1, rest - 1, aim, N, dp);
    } else {
        ans = walkCache(cur - 1, rest - 1, aim, N, dp) + walkCache(cur + 1, rest - 1, aim, N, dp);
    }
    dp[cur][rest] = ans;
    return ans;

}
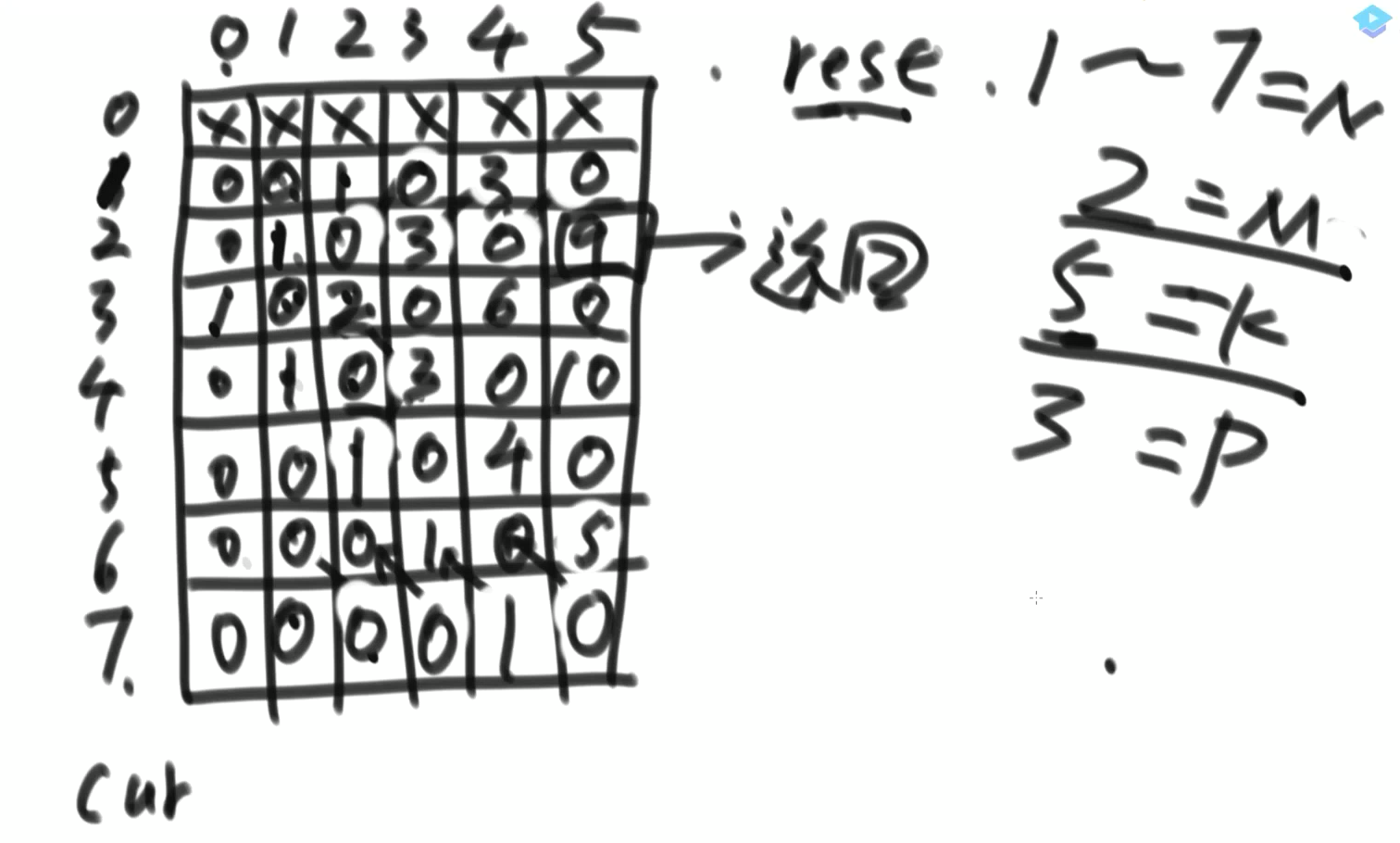
  7. 动态规划:动态规划是直接把暴力递归的思路直接架空，拿出所对应的确定的值进行计算1657607960651
    public static int robotWalkDP(int start, int aim, int K, int N) {
    if (N < 2 || start < 1 || start > N || aim < 1 || aim > N || K < 1) {
        return -1;
    }
    int[][] dp = new int[N + 1][K + 1];

    // cur已经到aim，而剩余步数也为0了
    dp[aim][0] = 1;
    // 处理其他的情况
    for (int rest = 1; rest <= K; rest++) {
        dp[1][rest] = dp[2][rest - 1];
        for (int cur = 2; cur < N; cur++) {
            dp[cur][rest] = dp[cur - 1][rest - 1] + dp[cur + 1][rest - 1];
        }
        dp[N][rest] = dp[N - 1][rest - 1];
    }
    return dp[start][K];
}

从左往右尝试模型:背包问题:

  1. 题目解释
    1. 给定两个长度都为N的数组weights和values，weight[i]和values[i]分别代表i号物品的重量和价值。
    2. 给定一个正数bag，表示一个载重bag的袋子，你装的物品不能超过这个重量。返回你能装下最多的价值是多少？
  2. 暴力递归
  3. 动态规划

从左往右尝试模型:数字字符转化问题

  1. 题目解释:
    1. 规定1和A对应，2和B对应，3和C对应…。那么一个数字字符比如”111”就可以转化为：“AAA”,“KA”,“AK”。
    2. 给定一个只有数字字符组成的字符串str,返回有多少种转化结果
  2. 思路：根据从左往右，我们划分多大，来尝试，比如111，我们尝试一个1，为”A”,剩下两个1去继续尝试。如果我们两个1尝试，就是”K”。三个1超过26字符，无法尝试。继续如此周而复始
  3. 暴力递归
  4. 动态规划

范围上的尝试模型:玩家抽取纸牌问题

  1. 题目解释:
    1. 给定一个整形数组arr，代表数值不同的纸牌排成一条线，玩家A和玩家B依次拿走每张纸牌。规定玩家A先拿，玩家B后拿，但是每个玩家每次只能拿走最左或最右的纸牌，玩家A和玩家B都绝顶聪明。请赶回最后获胜者的分数
    2. 绝顶聪明学术上的解释：双方玩家都会使得对方玩家在当前单独改变策略时，不会获得更大的收益。
  2. 暴力递归
  3. 动态规划

暴力递归到动态规划

  1. 题目=>找到暴力递归写法（尝试）
    1. 拥有重复解的前提下=>把可变参数
      1. 不讲究组织的形式，做缓存，那就是记忆化搜索的方法
      2. 精细化组织,那就是动态规划
    2. 如果暴力过程中没有枚举行为（即通过循环来求得值）
      1. 则记忆化搜索和动态规划的时间复杂度一致，没有必要从记忆化搜索再优化为动态规划
  2. 以背包问题举例，
    1. 我们每一个重量有要和不要两个选择，且都要递归展开。
    2. 那么我们的递归时间复杂度尾O(2^N)。
    3. 而记忆化搜索，根据可变参数得到的长为N价值为W的二维表，那么我们的时间复杂度为O(N*bag)。
    4. 如果递归过程中状态转移有化简继续优化的可能，例如枚举。那么经典动态规划可以继续优化，否则记忆化搜索和动态规划的时间复杂度是一样的

凑货币问题（重要）:该题是对动态规划完整优化路径的演示

  1. 题目解释:
    1. 有一个表示货币面值的数组arr，每种面值的货币可以使用任意多张。arr数组元素为正数，且无重复值。例如[7,3,100,50]这是四种面值的货币。
    2. 问：给定一个特定金额Sum，我们用货币面值数组有多少种方法，可以凑出该面值。例如P=1000,用这是四种面值有多少种可能凑出1000
  2. ways1为暴力递归的解题思路及实现
  3. ways2为暴力递归改记忆化搜索的版本
  4. ways3为记忆化搜索版本改动态规划的版本
  5. ways4为动态规划优化(排除重复枚举)的版本

贴纸问题

  1. 题目解释:
    1. 给定一个字符串str，给定一个字符串类型的数组arr。arr里的每一个字符串，代表一张贴纸，你可以把单个字符剪开使用，目的是拼出str来。
    2. 返回需要至少多少张贴纸可以完成这个任务。
    3. 例如：str=”babac”，arr={“ba”,”c”,”abcd”}
    4. 至少需要两张贴纸”ba”和”abcd”，因为使用这两张贴纸，把每一个字符串单独剪开，含有2个a，2个b，1个c。是可以拼出str的，所以返回2。
  2. 思路1 minStickers1：由于任何贴纸都可以剪切的很碎，跟贴纸的顺序没关系。那么目标str我们先进行排序，那么也不会有影响。babac排序为aabbc，我们再去选择贴纸，str被贴纸贴好后，剩下的接着排序，再选择……
    1. 由于我们的可变参数，只有一个目标字符串。但是目标字符串的可能性太多，没办法精细化动态规划。傻缓存的暴力递归已经是最优解了。所以只有一个可变参数，又存在重复解，那么傻缓存就是最优解。
  3. 思路2 minStickers2，我们每一张贴纸枚举所有可能的张数，后续过程不再考虑这张贴纸。但是方法一会好一点，因为只有一个可变参数。而方法二有两个可变参数，我们在设计递归的时候，尽量少的使用可变参数，这样我们缓存结构的命中率会提升

面试中设计暴力递归过程的原则

(怎么猜是不对的？)

  1. 每一个可变参数，一定不要比int类型更加复杂
    1. 比如可变参数是int a和int b 那么我们的缓存结构可以是a*b的二维数组。大小取决于a和b的范围
    2. 但是如果我们的可变参数是一个数组，int[] a。那么如果过多，我们不太容易设计那么大的缓存结构。如果只有一个这种可变参数就是原则2
    3. 不管什么问题，我们在脑海中想象可变参数就不会突破整形范围
  2. 原则1可以违反，让类型突破到一维线性结构，那必须是唯一可变参数。例如上述贴纸问题
  3. 如果发现原则1被违反，但没违反原则2。只需要做到记忆化搜索就是最优解
  4. 可变参数个数，能少则少

笔试面试过程中怎么设计暴力递归？

  1. 一定逼自己找到不违反原则情况下的暴力尝试！
  2. 如果你找到暴力尝试，不符合原则，马上舍弃，找新的！
  3. 如果某个题目突破了设计原则，一定极难极难，面试中出现的概率低于5%

常见的4种尝试模型

  1. 每一个模型背后都有很多题目

  2. 从左往右的尝试模型

    1. 例如背包问题

  3. 范围上的尝试模型

    1. 例如纸牌博弈问题

  4. 多样本位置全对应的尝试模型

    1. 两个字符串的最长公共子序列问题

  5. 寻找业务限制的尝试模型

    1. 四种模型中最难的一种，暂时只看process方法，process更改为动态规划的dp方法。后面会展开说明其他方法，

如何分析有没有重复解

  1. 列出调用过程，可以只列出前几层
  2. 有没有重复解，一看便知

暴力递归到动态规划的套路

  1. 你已经有了一个不违反原则的暴力递归，而且的确存在重复调用
  2. 找到哪些参数的变化会影响返回值，对每一个列出变化范围
  3. 参数间的所有组合数量，意味着缓存表(DP)大小
  4. 记忆化搜索的方法就是傻缓存，非常容易得到
  5. 规定好严格的表大小，分析位置的依赖顺序，然后从基础填写到最终解
  6. 对于有枚举行为的决策过程，进一步优化

动态规划的进一步优化

  1. 主要就是用来优化动态规划的单个位置的枚举行为
    1. 空间压缩
    2. 状态化简
    3. 四边形不等式
    4. 其他优化技巧

多样本位置全对应的尝试模型:两个字符串的最长公共子序列

  1. 题目解释:
    1. 例如“ab1cd2ef345gh”和“opq123rs4tx5yz”的最长公共子序列为“12345”。
    2. 即在两个字符串所有相等的子序列里最长的。所以返回子序列的长度5
    3. 假如”a123bc”和”12dea3fz”两个字符串，我们把这两个样本的下标一个作为行，一个作为列。
      1. 观察这样的结构所表示的意义。
      2. dp表这样设计就是str1从0到i位置，str2从0到j位置，两个位置的最长公共子序列。
      3. dp[i][j] 表示的含义是，str1字符串在i位置
      4. str2在j位置，两个最长公共子序列多长。
      5. 那么str1和str2的最长公共子序列，就是dp[str1.length][str2.length]
    4. 对于任何位置dp[i][j]:
      1. 如果str1的i位置和str2的j位置的最长公共子序列跟str1的i位置字符和str2的j位置字符无关，那么此时的最长公共子序列长度就是dp[i-1][j-1]
      2. 此时与str1的i位置结尾的字符有关系，和str2的j位置结尾的字符没关系。此时跟str2的j位置没关系，最长公共子序列式dp[i][j-1]
      3. 此时与str1的i位置结尾的字符没关系，和str2的j位置结尾的字符有关系。此时跟str1的j位置没关系，最长公共子序列式dp[i-1][j]
      4. 此时即与str1的i字符结尾，有关系。又与str2的j位置结尾，有关系。只有str1[i]==str2[j]才有可能存在这种情况，且为dp[i-1][j-1] + 1

寻找业务限制的尝试模型:咖啡问题

  1. 题目解释:
    1. 例题：给定一个数组，代表每个人喝完咖啡准备刷杯子的时间，只有一台咖啡机，一次只能洗一个杯子，时间耗费a，洗完才能洗下一杯。
    2. 每个咖啡杯也可以自己挥发干净，时间耗费b，咖啡杯可以并行挥发。
    3. 返回让所有咖啡杯变干净的最早完成时间。
    4. 三个参数：int[]arr , int a , int b（京东）
转载请注明来源，欢迎对文章中的引用来源进行考证，欢迎指出任何有错误或不够清晰的表达，可以邮件至 963614756@qq.com。

©2016-2020 HITlittlefox

Built with Hexo and 3-hexo theme