REST

回溯三部曲

1. 回溯函数模板返回值以及参数
   1. 习惯是函数起名字为backtracking
   2. 函数返回值一般为void
   3. 一般是先写逻辑，然后需要什么参数，就填什么参数。
   4. 回溯函数伪代码如下：

      void backtracking(参数)
      

2. 回溯函数终止条件
   1. 回溯函数终止条件伪代码如下：

      if (终止条件) {
          存放结果;
          return;
      }
      

3. 回溯搜索的遍历过程
   1. 回溯函数遍历过程伪代码如下：

      for (选择：本层集合中元素(树中节点孩子的数量就是集合的大小)) {
          处理节点;
          backtracking(路径，选择列表); // 递归
          回溯，撤销处理结果
      }
      

   2. for 循环可以理解是横向遍历:
      1. for 循环就是遍历集合区间，可以理解一个节点有多少个孩子，这个 for 循环就执行多少次。
   3. backtracking(递归)就是纵向遍历
      1. backtracking 这里自己调用自己，实现递归。
4. 回溯算法模板框架

   void backtracking(参数) {
       if (终止条件) {
           存放结果;
           return;
       }
       for (选择：本层集合中元素(树中节点孩子的数量就是集合的大小)) {
           处理节点;
           backtracking(路径，选择列表); // 递归
           回溯，撤销处理结果
       }
   }
   

回溯法解决的问题

组合问题：N 个数里面按一定规则找出 k 个数的集合
切割问题：一个字符串按一定规则有几种切割方式
子集问题：一个 N 个数的集合里有多少符合条件的子集
排列问题：N 个数按一定规则全排列，有几种排列方式
棋盘问题：N 皇后，解数独等等

本题还需要 startIndex 来控制 for 循环的起始位置，对于组合问题，什么时候需要 startIndex 呢？

我举过例子，如果是一个集合来求组合的话，就需要 startIndex，例如：77. 组合 ，216. 组合总和 III 。

如果是多个集合取组合，各个集合之间相互不影响，那么就不用 startIndex，例如：17. 电话号码的字母组合

注意以上我只是说求组合的情况，如果是排列问题，又是另一套分析的套路，后面我再讲解排列的时候就重点介绍。

用递归控制 for 循环嵌套的数量！

把回溯问题抽象为树形结构，可以直观的看出其搜索的过程：for 循环横向遍历，递归纵向遍历，回溯不断调整结果集。

剪枝优化

把问题抽象为一个树形结构，可以看到需要剪枝的部分
剪枝精髓是：for 循环在寻找起点的时候要有一个范围，如果这个起点到集合终止之间的元素已经不够 题目要求的 k 个元素了，就没有必要搜索了。

求子集问题和 77. 组合 和 131. 分割回文串 又不一样

1. 如果把 子集问题、组合问题、分割问题都抽象为一棵树的话，那么组合问题和分割问题都是收集树的叶子节点，而子集问题是找树的所有节点！
2. 其实子集也是一种组合问题，因为它的集合是无序的，子集 {1,2} 和 子集 {2,1} 是一样的。
3. 那么既然是无序，取过的元素不会重复取，写回溯算法的时候，for 就要从 startIndex 开始，而不是从 0 开始！
4. 什么时候 for 可以从 0 开始呢？
   1. 求排列问题的时候，就要从 0 开始，因为集合是有序的，{1, 2} 和 {2, 1} 是两个集合
5. 子集是收集树形结构中树的所有节点的结果。
6. 而组合问题、分割问题是收集树形结构中叶子节点的结果。

求组合的情况

1. 如果是一个集合来求组合的话，就需要 startIndex，
   1. 例如：回溯算法：求组合问题！， 回溯算法：求组合总和！ 。
2. 如果是多个集合取组合，各个集合之间相互不影响，那么就不用 startIndex，
   1. 例如：回溯算法：电话号码的字母组合

理解 “树层去重” 和 “树枝去重” 非常重要。

难点在于 集合（数组 candidates）有重复元素，但还不能有重复的组合。

1. 一些同学可能想了：我把所有组合求出来，再用 set 或者 map 去重，这么做很容易超时！
2. 所以要在搜索的过程中就去掉重复组合。
3. 去重，其实就是使用过的元素不能重复选取
4. 组合问题可以抽象为树形结构，那么 “使用过” 在这个树形结构上是有两个维度的，
   1. 一个维度是同一树枝上使用过，
   2. 一个维度是同一树层上使用过
5. 例题1:
   1. 回看一下题目，元素在同一个组合内是可以重复的，怎么重复都没事，但两个组合不能相同。
   2. 所以我们要去重的是同一树层上的 “使用过”，同一树枝上的都是一个组合里的元素，不用去重。
   3. 为了理解去重我们来举一个例子，candidates = [1, 1, 2], target = 3，（方便起见 candidates 已经排序了）
   4. 强调一下，树层去重的话，需要对数组排序！
   5. 选择过程树形结构如图所示：
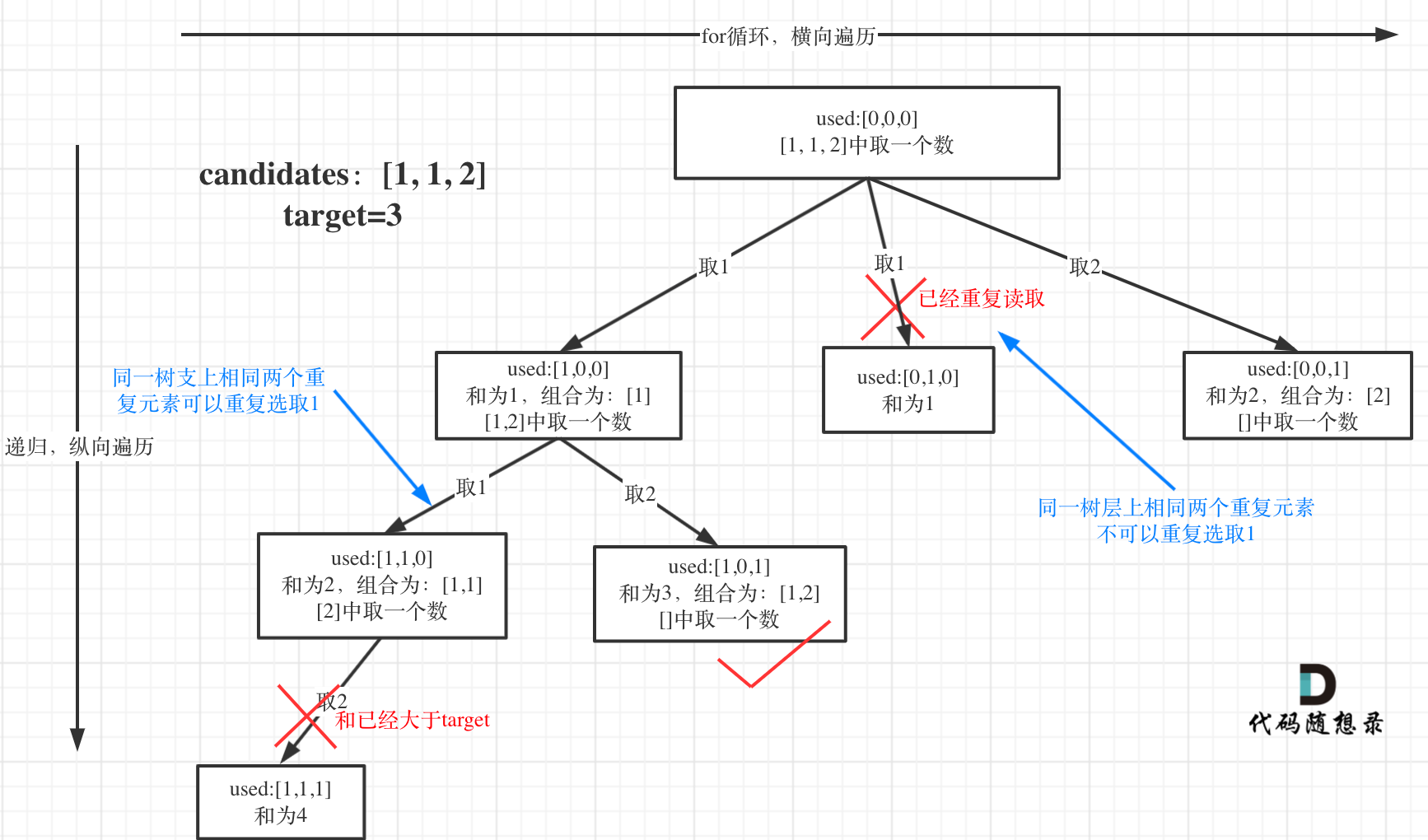
   6. 加一个 bool 型数组 used，用来记录同一树枝上的元素是否使用过。这个集合去重的重任就是 used 来完成的。
   7. 也就是说,树层去重:for循环中需要对重复值进行continue,递归时不需要
6. 例题2:
   1. 同样也是树层去重
   2. 

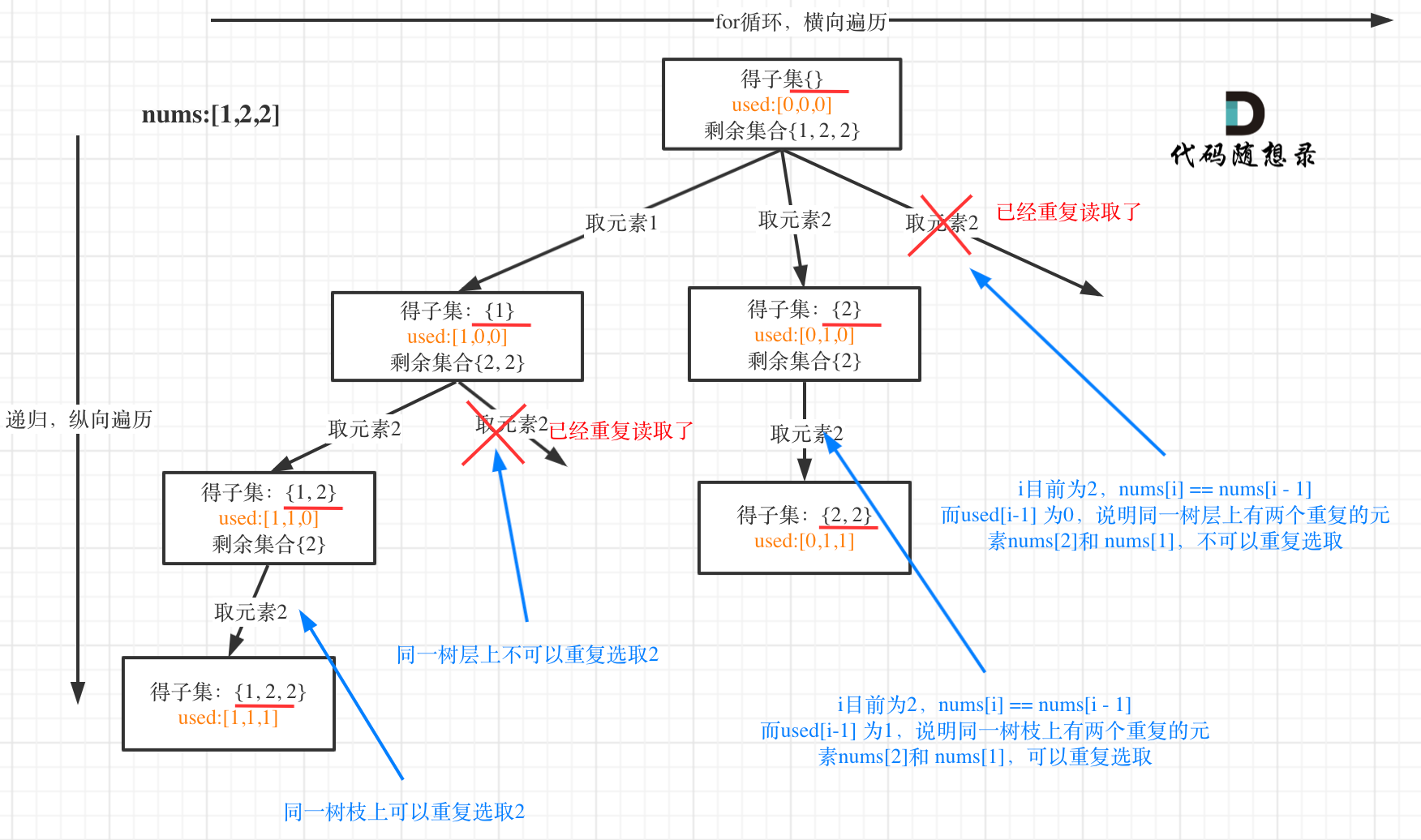
数组，set，map 都可以做哈希表，而且数组干的活，map 和 set 都能干，但如果数值范围小的话能用数组尽量用数组。

如果要对树层中前一位去重，就用 used[i - 1] == false，如果要对树枝前一位去重用 used[i - 1] == true。

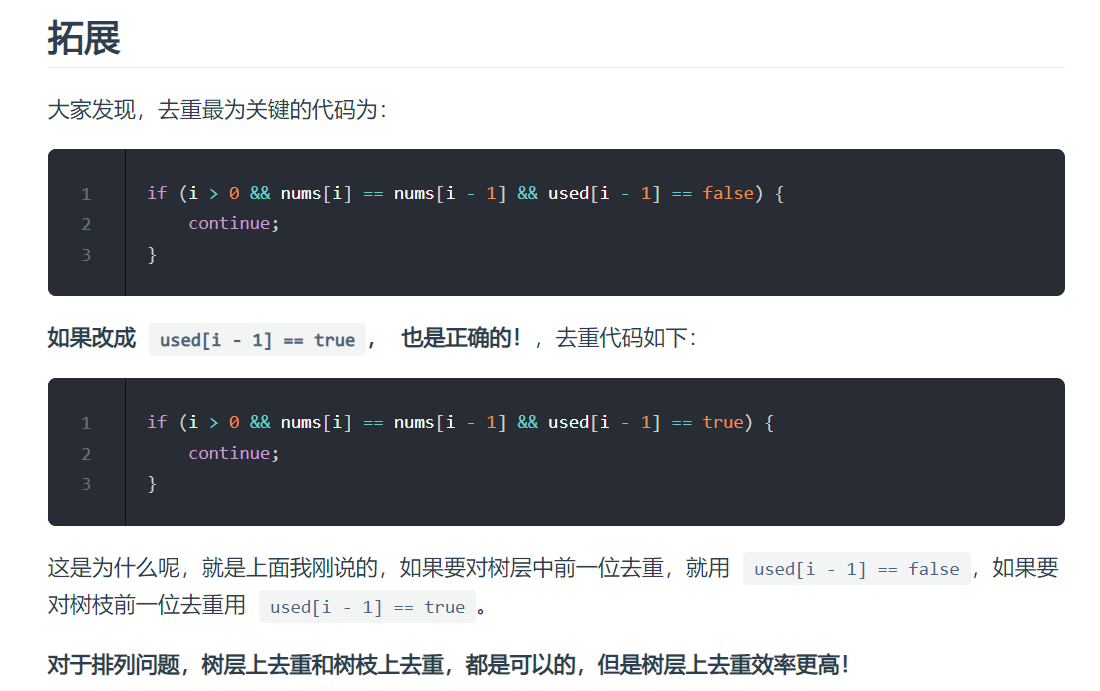
之前讲解回溯算法的时候，一般函数返回值都是 void，这次为什么是 bool 呢？

因为我们只需要找到一个行程，就是在树形结构中唯一的一条通向叶子节点的路线

---

转载请注明来源，欢迎对文章中的引用来源进行考证，欢迎指出任何有错误或不够清晰的表达，可以邮件至 963614756@qq.com。